By

题目描述

大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项

题目解析

解斐波那契数列最基本的方法就是递归和迭代，但是递归要做太多重复的事情，效率很低不考虑。用基本的迭代方法，复杂度是O(n)。一开始令f1=0，f2=1，当n=0时，直接返回f1；当n=1时，交换f1、f2；之后开始正常的迭代过程，每次前移一个单位，f1为f2的后一个数，代码如下：

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int Fibonacci(int n) {
        int f1=0,f2=1;
        while(n-->0){
            f1+=f2;
            f2=f1-f2;
        }
        return f1;
    }
};

考虑到解斐波那契数列可以用矩阵快速幂的方法，时间复杂度O(logn)比直接进行迭代要更优，这里考虑用矩阵快速幂来解决本题，函数如下：

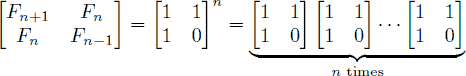
首先我们先讨论整数的快速幂问题，比如A^9 = A*A*A*A*A*A*A*A*A = A*((A^2)^2)^2，A平方后，再平方，再平方，然后乘上剩下的一个A，要乘4次，比直接迭代要乘以9次来的快。

当n为自然数时，
x*(2^n) = x<<n
x/(2^n) = x>>n
当x=2^n时，a%x = a&(x-1)

于是可以写出整数快速幂的代码如下：

1
2
3
4
5
6
7
8
9
10
11
int fast_mod(int x,int n){
    int ans=1;
    while(n){
        if(n&1){
            ans*=x;
        }
        x*=x;
        n>>=1;
    }
    return ans;
}

其实矩阵的快速幂和整数的快速幂是一样的，只是在乘法过程中我们要自己写一个矩阵的相乘函数。我们定一个一个结构体matrix来保存矩阵，初始化base和ans，base相当于整数快速幂中的x，ans相当于整数快速幂中的ans，求出矩阵[[1,1],[1,0]]的n次方，以此来求斐波那契数列。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    int Fibonacci(int n) {
        base.b[0][0]=base.b[0][1]=base.b[1][0]=1;
        base.b[1][1]=0;
        ans.b[0][0]=ans.b[1][1]=1;
        ans.b[0][1]=ans.b[1][0]=0;
        while(n){
            if(n&1){
                ans=multi(ans,base);
            }
            base=multi(base,base);
            n>>=1;
        }
        return ans.b[0][1];
    }
private:
    struct matrix{
        int b[2][2];
    }base,ans;
    matrix multi(matrix m1,matrix m2){
        matrix matx;
        for(int i=0;i<2;i++){
            for(int j=0;j<2;j++){
                matx.b[i][j]=0;
                for(int k=0;k<2;k++){
                    matx.b[i][j]+=m1.b[i][k]*m2.b[k][j];
                }
            }
        }
        return matx;
    }
};